Funktionen
Definition
Funktionen sind ein mathematisches Konstrukt, welche jedes Element \(x\) einer Definitionsmenge \(D\) genau einem Element \(y\) aus der Zielmenge \(Z\) zuordnet. Sie sind ein elementarer Bestandteil der Physik und werden in allen Bereichen häufig genutzt.
Man schreibt die Definition einer Funktion \(f\) wie folgt
\begin{align*} f: \ & D \to Z \\ & x \mapsto y \end{align*}Dabei ist x \mapsto y die Funktionsvorschrift, also der Teil, welcher besagt, was eine Funktion mit einer Eingabe machen soll.
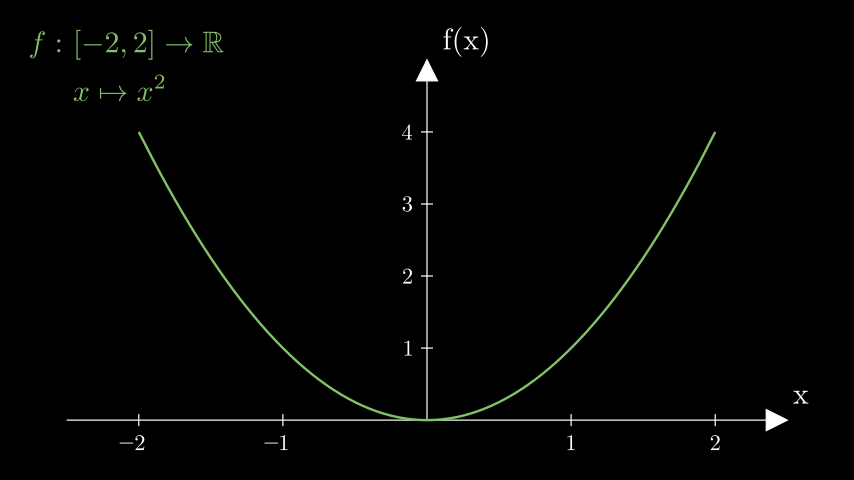
Im Folgenden sind Beispiele von Funktionen zu sehen, welche alle die selbe Funktionsvorschrift haben, nämlich x \mapsto x^2 , sich jedoch durch einen jeweils anderen Definitionsbereich und Wertebereich unterscheiden.
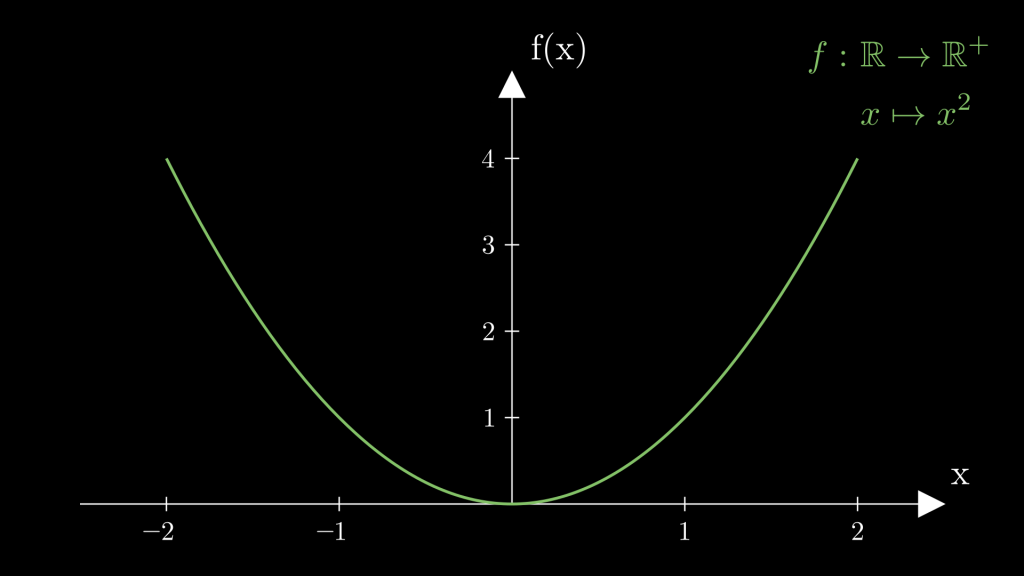
Dabei ist zu erwähnen, dass die gewohnte Normalparabel f: \mathbb{R} \to \mathbb{R} \,, x \mapsto x^2 nicht gezeigt wurde, da dies der bekannteste Fall ist, welcher in der Schule behandelt wird. Dabei wird jeder reellen Zahl \(x\) ein Wert \(y = x^2\) zugeordnet.
Dabei bedeutet Stetigkeit sehr vereinfacht gesagt (nicht mathematisch), dass wenn man den Graphen der Funktion mit einem Stift zeichnet, diesen ohne den Stift vom Papier abzuheben zeichnen kann.
Injektive, surjektive und bijektive Funktionen
Funktionen können verschiedenen Eigenschaften bezüglich ihrer Definition der Werte- und Definitionsmenge haben.
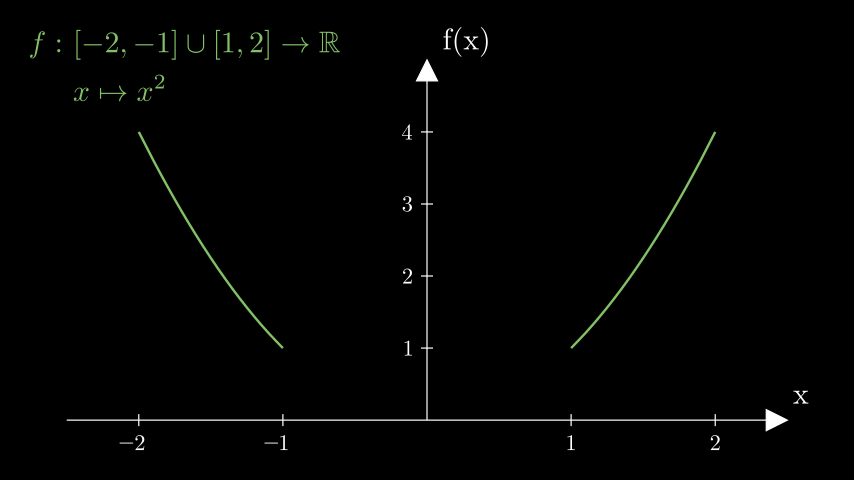
Injektiv: Jedes Element der Wertemenge hat höchstens ein Urbild. Das bedeutet, dass es manche Elemente \(y\) in der Wertemenge gibt, welche keine Zuordnung eines Elementes \(x\) aus der Definitionsmenge sind.
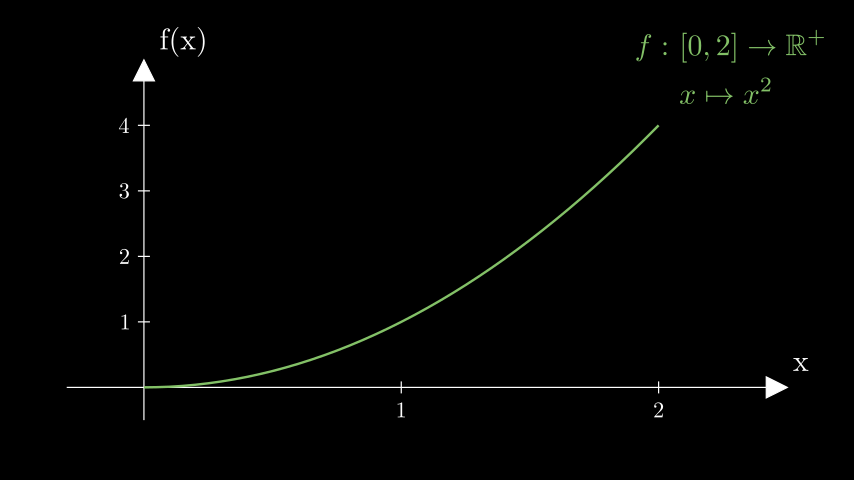
Surjektiv: Jedes Element \(y\) aus der Wertemenge ist die Zuordnung mindestens eines Elementes \(x\) aus der Definitionsmenge.
Bijektiv: Eine bijektive Abbildung ordnet jedem Element \(x\) aus der Definitionsmenge genau einen Wert \(y\) aus der Wertemenge zu.
Anhand der folgenden Graphen werden die Eigenschaften näher erläutert.
Da jedes \(y\) höchstens ein Urbild haben darf, ist es erlaubt, das manche \(y\) von keinem \(x\) die Funktionswerte sind. Deshalb ist hier der Wertebereich mit \mathbb{R} gewählt. Denn durch eine Parabel werden nur positive Werte und die \(0\) erreicht. Aber negative Werte, welche in der Menge \mathbb{R} enthalten sind, können niemals durch eine Parabel erhalten werden.
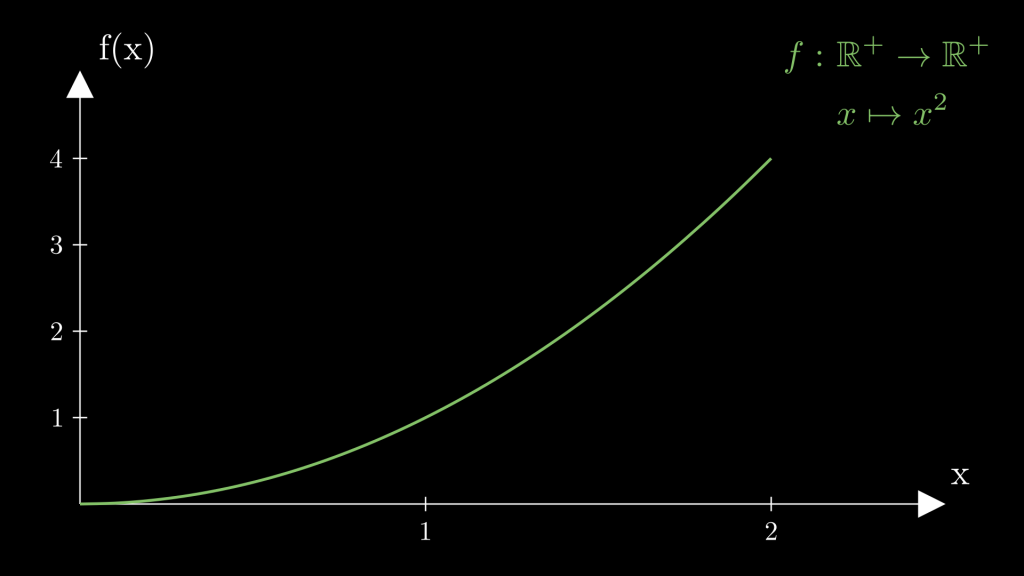
Hier wird jedes Element \(y\) von mindestens einem Wert \(x\) aus der Definitionsmenge getroffen. Das bedeutet gleichzeitig, dass 2 verschiedene Werte \(x1_1, x_2\) auf den selben Wert \(y\) abgebildet werden. Als Beispiel können die Werte \(x_1 = -2\) und \(x_2 = 2\) betrachtet werden. Beide Werte quadriert ergeben den Wert \(4\).
Eine bijektive Funktion ist eine Funktion, welche sowohl injektiv als auch surjektiv ist. Das bedeutet, dass jedes \(x\) auf genau ein \(y\) abgebildet wird, und kein Wert \(y\) kein Urbild hat.
Verkettung von Funktionen (Komposition)
Seien die Funktionen f: A \to B und g: B \to C gegeben. So kann die Verkettung der beiden Funktionen g \circ f gebildet werden durch
\begin{align*} g \circ f: \ & A \to C \\ & x \mapsto (g \circ f)(x) := g\big(f(x)\big) \end{align*}Man kann also sehen, dass die Verkettung zweier Funktionen einfach das einsetzen der einen Funktion in die andere Funktion ist.
Beispiel
Seien nun die Funktionen \(f(x) = \sin(x)\) und \(g(u) = u^2 + 2u\) gegeben. So lautet die Komposition \((g \circ f)(x)\):
(g \circ f)(x) = \sin^2(x) + 2 \sin(x)Umkehrfunktion
Eine Umkehrfunktion zur Funktion f: D \to Z wird mit f^{-1} bezeichnet, und durch f^{-1}: Z \to D definiert. Dabei ist die hochgestellte „-1“ keine Potenz, sondern das Symbol der Umkehrfunktion. Die Anwendung der Umkehrfunktion auf einen Funktionswert ergibt also wieder das Urbild. Es gilt also f(y) = x \,.
Verweise
Zum Thema „Funktionen“ verweisen wir gerne auf
- ein YouTube-Video, welches besonders für Anfänger geeignet ist, welche gerade von der Schule kommen.
- das Lernportal der Georg-August-Universität Göttingen. Diese Seite ist besonders für Beispiele und die Themen „Injektivität, Surjektivität und Bijektivität“ gedacht.