Komplexe Zahlen
Definition
Die komplexe Einheit \(i\) ist durch
i^2 = -1
definiert. Man sieht häufig die Form \(i = \sqrt{-1}\). Man kann dabei sagen, dass \(\sqrt{-1}\) durch \(i\) definiert wird, jedoch kann diese Form zu folgendem Fehler führen:
-1 = i^2 = i \cdot i \neq \sqrt{-1} \cdot \sqrt{-1} = \sqrt{-1 \cdot (-1)} = \sqrt{1} = 1
Deshalb wird häufig folgende Methode verwendet, um komplexe Zahlen umzuschreiben
\begin{align*} && z &:= \sqrt{-16} \\ \Rightarrow && z^2 &= -16 = i^2 \cdot 16 \\ \Rightarrow && z &= i \cdot \sqrt{16}\\ \Rightarrow && z &= 4i \end{align*}
Im Allgemeinen kann eine komplexe Zahl durch \begin{equation} z = a + i \cdot b \end{equation} definiert werden. Dabei ist \mathcal{Re}(z) = a der Realteil und \mathcal{Im}(z) = b der Imaginärteil.
Die Menge der komplexen Zahlen wird mit \mathbb{C} bzeichnet.
Komplexe Konjugation
Die komplexe Konjugation \overline{z} einer komplexen Zahl z = a + i b ist definiert als
\begin{equation} \overline z = a-i b \end{equation}Es ist also nur ein Vorzeichenwechsel des Imaginärteils. Dies wird später noch wichtig.
Eulerformel
Eine Komplexe Zahl kann auch in einer anderen Form dargestellt werden, nämlich der Eulerform. Während obige Form z = a + ib eine Analogie zum kartesischen Koordinatensystem ist, wobei \(a\) die Analogie zu den \(x\)-Werten und \(b\) die Analogie zu den \(y\)-Werten ist, wird die Eulerform im Folgenden eine Analogie zu den Polarkoordinaten darstellen.
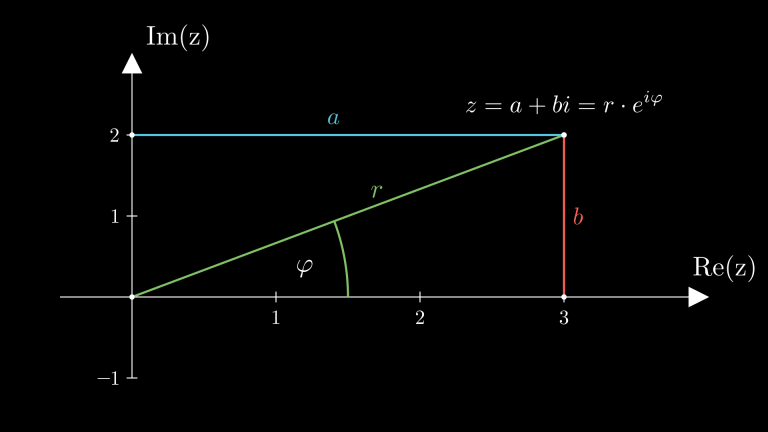
Dazu betrachten wir folgende Grafik, in der beispielhaft eine komplexe Zahl eingetragen ist.
Diese ist in der Grafik zur Veranschaulichung als \(z = 3 + 2i\) gewählt, jedoch möchten wir zur Rechnung eine allgemeine komplexe Zahl z = a + b i betrachten. Somit können wir nun folgenden Zusammenhang feststellen:
\begin{align*} a = r \cdot \cos(\varphi) \\ b = r \cdot \sin(\varphi) \end{align*}Das bedeutet, wir können eine komplexe Zahl im Allgemeinen auch durch
\begin{equation} z = r \cdot \big( \cos(\varphi) + i \cdot \sin(\varphi) \big) \end{equation}darstellen.
Nun können wir uns auch folgenden Zusammenhang durch die Taylorreihe der komplexen Exponentialfunktion herleiten:
\begin{align*} e^{ix} &= \sum_{k=0}^\infty \dfrac{(ix)^k}{k!} \\ &= \sum_{p=0}^\infty \dfrac{(ix)^{2p}}{(2p)!} + \sum_{q=0}^\infty \dfrac{(ix)^{2q+1}}{(2q+1)!} \\ &= \sum_{p=0}^\infty (-1)^p \dfrac{x^{2p}}{(2p)!} + i \cdot \sum_{q=0}^\infty (-1)^q \dfrac{x^{2q+1}}{(2q+1)!} \\ &= \cos(x) + i \cdot \sin(x) \end{align*}Zu aller erst sei gesagt, dass die Exponentialfunktion gewissermaßen durch ihre Taylorreihe e^x = \sum_{k=0}^\infty \dfrac{x^k}{k!} definiert ist. Somit ist die erste Gleichung in obiger Rechnung eine reine Definition. In der zweiten Gleichung wurde die Summe aufgeteilt. Und zwar in die Terme mit geradem und ungeradem Exponenten. Warum dies erlaubt ist, ist an der kommutativen Eigenschaft der Addition zu sehen. Die Summe \(1+2+3+4+5+6+7+8\) ist die selbe, wie die Summe \( (2+4+6+8) + (1+3+5+7) \). Und da die Zahl \(2p \ (p \in \mathbb{Z})\) immer gerade ist, und die Zahl \(2q+1 \ (q \in \mathbb{Z})\) immer ungerade ist, ist die Umformung zur zweiten Gleichung zulässig.
In der dritten Gleichung wird die Definition \(i^2 = -1\) genutzt. Denn daraus folgt, dass i^{2p} = (-1)^p und i^{2q+1} = i \cdot (-1)^q .
Die letzte Gleichung kann gewissermaßen als die Definition von Sinus und Cosinus betrachtet werden. Diese sind die Taylorreihen der beiden Funktionen.
Wenn wir nun die beiden Gleichungen
\begin{align}
z &= r \cdot \big( \cos(\varphi) + i \cdot \sin(\varphi) \big) \\
e^{i\varphi} &= \cos(\varphi) + i \cdot \sin(\varphi)
\end{align}
miteinander vergleichen, fällt auf, dass wir eine komplexe Zahl auch allgemein durch
darstellen können. Dies ist die Eulerformel!
Um dies beispielsweise anhand des Kosinus zu untermauern, wird im Folgenden eine Animation gezeigt, welche den Realteil einer komplexen Zahl, welche sich auf dem Einheitskreis bewegt, gegen den Drehwinkel aufgetragen. Daraus entsteht wiederrum der Graph des Kosinus.
An dieser Stelle wird häufig die Frage gestellt, warum die Darstellung über Sinus und Cosinus nicht ausreiche. Dies hat den Grund, dass mit der Exponentialfunktion wesentlich einfacher zu rechnen ist, als mit Sinus und Cosinus.
Als Beispiel betrachten wir z^2 = (a + bi)^2 . In der Darstellung über Sinus und Cosinus erhalten wir durch die erste binomische Formel z^2 = r \cdot \big(\cos^2(\varphi) + 2 \cos(\varphi) \sin(\varphi) – \sin^2(\varphi)\big) . Über die Eulerformel erhalten wir jedoch z^2 = e^{2i \varphi} . In sehr langen Rechnung erspart man sich somit einige Terme und ist nicht auf die Additionstheoreme von Sinus und Cosinus angewiesen.
Rechenregeln
Betrag einer komplexen Zahl
Der Betrag einer komplexen Zahl z = a + i b wird definiert durch
\begin{equation} |z| = \sqrt{a^2 + b^2} \end{equation}Der Betrag einer komplexen Zahl gibt somit den Abstand dieser Zahl zum Ursprung an. In der Eulerdarstellung mit z = r \cdot e^{i\varphi} ist der Betrag also direkt an dem \(r = |z|\) ablesbar! Daraus kann auch gefolgert werden, dass \cos^2(x) + \sin^2(x) = 1 mit x \in \mathbb{R} .
Es gilt jedoch auch folgender Zusammenhang, welcher z.B. in der theoretischen Quantenmechanik häufig genutzt wird: z \cdot \overline z = (a + i b) \cdot (a – i b) = a^2+iab-iab-i^2b^2 = a^2 + b^2 = |z|^2 \quad \text{oder} \quad z \cdot \overline z = r^2 e^{i \varphi – i\varphi} = r^2 e^0 = r^2 = |z|^2 \,.
Winkel zur Realteil-Achse
Aus der Schule kennen wir den Zusammenhang aus einem rechtwinkligen Dreieck tan(\varphi) = \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \,. Somit können wir den Dreh-Winkel einer komplexen Zahl z = a+bi in Relation zur Realteilachse durch
\begin{equation} \varphi = \arctan\left(\dfrac{b}{a}\right) \end{equation}berechnen.
Addition und Subtraktion
Komplexe Zahlen können, wie auch die reellen Zahlen, addiert, subtrahiert, multipliziert und dividiert werden. Seinen dazu z_1, z_2 \in \mathbb{C} komplexe Zahlen mit z_1 = a + i b \,, \ z_2 = c + i d . Dann gilt für die Addition von \(z_1\) und \(z_2\):
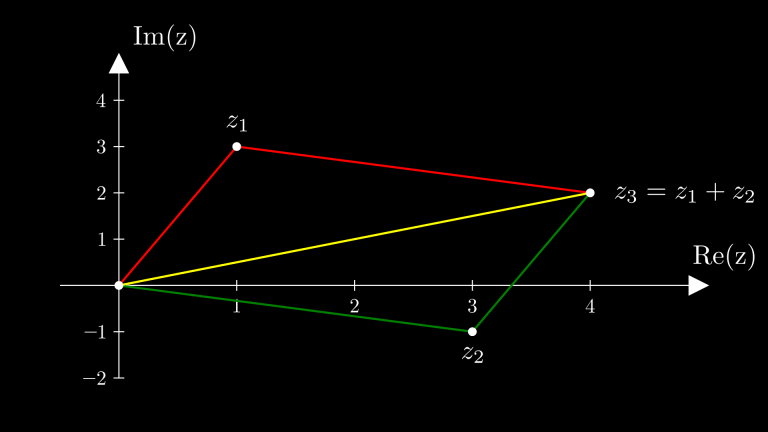
z_1 + z_2 = (a + c) + i \cdot (b + d)Grafisch kann man sich die Addition zweier komplexer Zahlen ähnlich wie die Addition zweier Vektoren vorstellen. Dazu betrachten wir folgende Grafik, in der die komplexen Zahlen \(z_1 = 1 + 3i\) und \(z_2 = 3 – i\) miteinander addiert wurden, was die komplexe Zahl \(z_3 = 4 + 2i\) ergibt.
Grafisch ähnelt es deshalb der Vektoraddition, da dieselbe Grafik auch durch die Addition der Vektoren \vec v_1 = \hat e_x + 3\hat e_y und \vec v_2 = 3\hat e_x – \hat e_y entstehen würde.
Die Subtraktion zweier komplexer Zahlen funktioniert analog. Also gilt allgemein mit obiger Definition z_1 = a + i b \,, \ z_2 = c + i d folgender Zusammenhang: z_1 – z_2 = (a-c) + i \cdot (b – d) .
Multiplikation
Ohne es wirklich erklärt zu haben, wurde oben schon öfter mit komplexen Zahlen multipliziert.
Wir betrachten erneut zwei komplexe Zahlen nach obiger Definition z_1 = a + i b \,, \ z_2 = c + i d . Somit gilt für ihre Multiplikation miteinander z_1 \cdot z_2 = ac+i \cdot (ad + bc)-bd
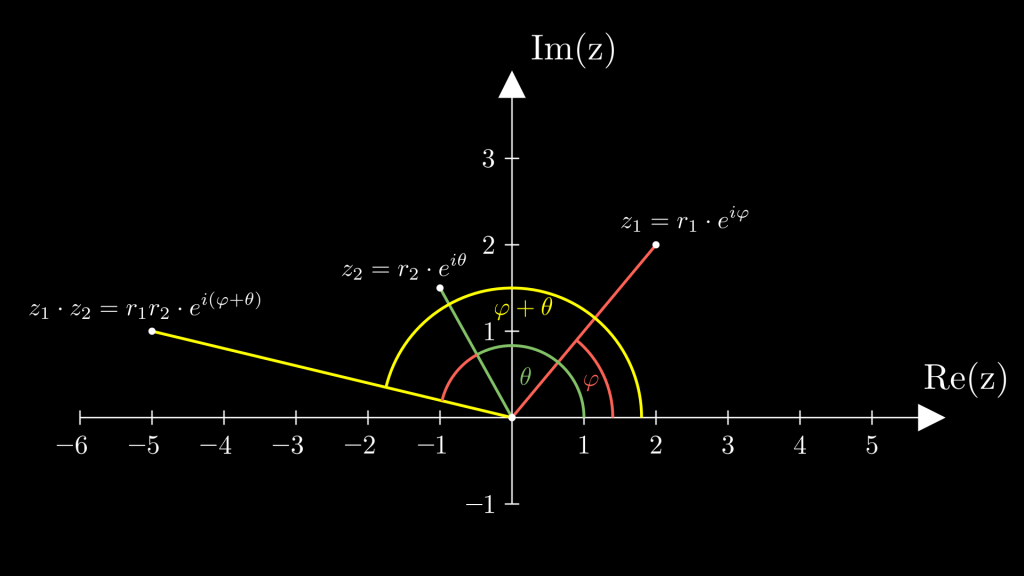
Grafisch kann man sich die Multiplikation als Drehung der einen komplexen Zahl um den Winkel der anderen komplexen Zahl vorstellen, wobei der Betrag des Ergebnisses der Multiplikation der Beträge der beiden Multiplikatoren ist. Dies kann wunderbar anhand der Eulerformel gezeigt werden. Für z_1 = r_1 \cdot e^{i\varphi} und z_2 = r_2 \cdot e^{i\theta} gilt z_1 \cdot z_2 = r_1 \cdot e^{i\varphi} \cdot r_2 \cdot e^{i\theta} = r_1 r_2 \cdot e^{i \cdot (\varphi + \theta)} \,.
Diese Anschauung ist in folgender Grafik dargestellt.
Division
Bei der Division zweier komplexer Zahlen z_1 = a + i b \,, \ z_2 = c + i d verwendet man einen Trick. Man erweitert den Bruch mit der komplex Kojugierten Zahl aus dem Nenner, um im Nenner eine reelle Zahl stehen zu haben, nämlich den Betrag der komplexen Zahl aus dem Nenner zum Quadrat. Dies geschieht wie folgt:
\dfrac{z_1}{z_2} = \dfrac{a + i b}{c + id} = \dfrac{(a + i b) \cdot (c – i d)}{(c + i d) \cdot (c – i d)} = \dfrac{ac + i \cdot (b c – a d) + b d}{c^2 + d^2} \,.Verweise
Für das Thema „Komplexe Zahlen“ verweisen wir gerne auf folgende Quellen:
- Lernportal der Universität Göttingen (mit Übungsaufgaben und Lösungen)
- Wikipedia (Komplexe Zahlen)
- Wikipedia (Eulerformel)
Es ist auch ein Video von 3Blue1Brown zu empfehlen. Dieser Kanal ist generell für das Physik- und Mathematik-Studium und natürlich auch für alle Interessierte zu empfehlen.
Des Weiteren kann das Video von Mathologer empfohlen werden, in dem grafisch sehr anschaulich die Beziehung e^{i\pi} = -1 gezeigt wird.
Zu Taylorreihen existiert eine Seite der hochschuldidatik-physik.de. Wir verweisen dabei aber natürlich auch gerne auf das Lernportal der Georg-August-Universität Göttingen und einem weiteren Video von 3Blue1Brwon.