Wegintegral
Wegintegrale sind ein wichtiger Bestandteil in der Physik, welche aber in erster Linie rein mathematische Konstrukte sind.
Sie werden beispielsweise oft genutzt, um die verrichtete Arbeite eines Körpers entlang eines Weges \(\gamma(t)\) innerhalb eines Kraftfeldes \(\vec F(x,y)\) zu berechnen. Dabei sind \(x,y\) Ortskoordinaten und \(t \in [a,b] \text{ mit } a,b \in \mathbb{R}\) ein Parameter zur Parametrisierung des Weges.
Wegintegrale erster Art
Es gibt Wegintegrale erster und zweiter Art. Im Endeffekt unterscheiden sie sich nur davon, ob wir einen Weg durch ein skalares Feld \(f\) oder einem Vektorfeld \(\vec F\) betrachten.
Sei \(\vec \gamma: [a,b] \to \mathbb{R}^n\) unser \(n\)-dimensionaler Weg, welchen wir „entlang gehen“ wollen. Mit unserem skalaren Feld \(f : \mathbb{R}^n \to \mathbb{R}\) ist dann das Wegintegral definiert durch
\begin{equation} \int_\gamma f \cdot ds := \int_{a}^{b} f(\vec \gamma(t)) \cdot \left| \left| \frac{d\vec\gamma}{dt} \right| \right|_2 dt \,. \end{equation}Dabei ist \(||\cdot||_2\) die euklidische Norm. Diese ist für einen \(n\)-diensionalen Vektor definiert als \left| \left| \vec v \right| \right|_2 = \left( \sum_{i=1}^{n} v_i^2 \right)^{\frac{1}{2}} .
Beispielaufgabe mit Lösung
Sei f(x,y) = x^2+y und \vec \gamma = \begin{pmatrix} t \\ -t\end{pmatrix} der betrachtete Weg mit t \in [a,b]; a,b \in \mathbb{R} . Berechnen Sie nun das Wegintegral \int_\gamma f \cdot ds .
Zuerst bilden wir die Ableitung von \(\vec \gamma(t)\) nach \(t\). Diese lautet
\dot{\vec \gamma}(t) = \begin{pmatrix} 1 \\ -1 \end{pmatrix} \,.
Daraus bilden wir nun den Betrag
\left| \left| \dfrac{\vec \gamma}{dt} \right| \right|_2 = \sqrt{2} \,.Um das Wegintegral auszurechnen, benötigen wir noch f\big(\vec \gamma(t)\big) = t^2-t .
Nun können wir das Wegintegral ausrechnen:
\begin{align*} \int_\gamma f \cdot ds &= \int_{a}^{b} f(\vec \gamma(t)) \cdot \left| \left| \frac{d\vec\gamma}{dt} \right| \right|_2 dt \\ &= \int_a^b (t^2-t)\cdot \sqrt{2} dt \\ &= \sqrt{2} \cdot \left[ \frac{1}{3} t^3 – \frac{1}{2} t^2 \right]_a^b \\ &= \sqrt{2} \cdot \left[ \frac{1}{3} (b^3-a^3) – \frac{1}{2} (b^2-a^2) \right] \end{align*}Wenn die Aufgabe es verlangen würde, könnten jetzt noch für \(a, b\) feste Zahlen eingesetzt werden, wie z.B. \(a = 0, b=2\). Daraus folgt
\int_\gamma f \cdot ds =\sqrt{2} \cdot \left[ \frac{1}{3} \cdot 2^3 – \frac{1}{2} \cdot 2^2 \right] = \sqrt{2} \cdot \frac{2}{3} \approx 0,94Wegintegrale zweiter Art
Im Folgenden ist ein Video zu Wegintegralen gezeigt. Zum besseren Verständnis für die weitere Erklärung lohnt es sich, dieses Video mindestens ein mal angesehen zu haben.
Das Wegintegral \( \int_\gamma \vec F \cdot d\vec s \) mit dem Weg \(\vec \gamma: [a,b] \to \mathbb{R}^n\) durch das Vektorfeld \(\vec F : \mathbb{R}^n \to \mathbb{R}^n\) ist definiert als
\int_\gamma \vec F \cdot d\vec s := \int_a^b \vec F(\vec \gamma(t)) \cdot \frac{d\vec \gamma(t)}{dt} dtDabei kann \(\frac{d\vec \gamma(t)}{dt}\) als \(\dot{\vec \gamma}(t)\) geschrieben werden.
Man kann sich die Formel, wie im Video gezeigt, vorstellen, als würde man das infinitesimale Wegelement \(ds\) durch \(d\gamma\) ersetzen, und mit dem Bruch \(\frac{dt}{dt}\) erweitern, welcher selbstverständlich \(1\) ist.
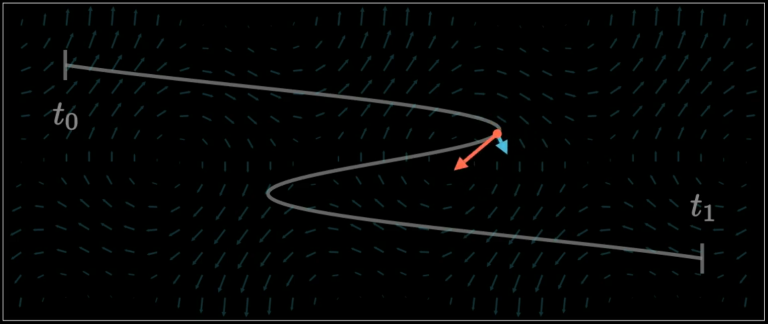
Danach ist im Video zu sehen, wie zwei Pfeile von einem gemeinsamen Punkt aus den Pfad \(\vec \gamma\) entlangfahren. Dabei symbolisiert der blaue Pfeil das Vektorfeld an einem dem jeweiligen Punkt auf dem Pfad \(\vec \gamma(t)\), während der rote Pfeil die Tangente des Pfades am jeweiligen Punkt repräsentiert.
Anhand der obigen Formel ist ersichtlich, dass das Wegintegral von dem Skalarprodukt aus dem Vektor des Vektorfeldes \(\vec F\) an einem gewissen Punkt \(\vec \gamma(t)\) und der Tangente des Weges \(\dot{\vec \gamma}(t)\) abhängt. Dies ist der Integrand \(\vec F(\vec \gamma(t)) \cdot \frac{d\vec \gamma(t)}{dt}\). Dieses Skalarprodukt ist als weiße Linie unter dem Pfad aufgetragen.
Gleichzeitig gilt aber auch, dass das Skalarprodukt zweier Vektoren genau dann Null beträgt, wenn diese senkrecht aufeinander stehen. Dies ist gut an den Kurven des Weges zu sehen. Denn genau dort stehen die beiden Vektoren senkrecht aufeinander, wodurch das Skalarprodukt an dieser Stelle Null wird. Dies ist gut im kleinen Diagramm in der unteren rechten Ecke zu sehen, wo die Vektoren extra im \(x\)-\(y\)-Koordinatensystem dargestellt werden. Dadurch trägt dieser Punkt nichts zum Wegintegral bei.
Schlussendlich ist das Wegintegral das Integral über obiges Skalarprodukt vom Anfang bis zum Ende des Weges. Man kann es sich also vorstellen, als ob alle Skalarprodukte auf dem Weg aufsummiert werden. Das ist auch der Grund, warum senkrechte Vektoren im Integral nichts zum Wert des Wegintegrals beitragen.
Somit ist die Fläche unter der weißen Linie der Wert des Wegintegrals.
Beispielaufgabe
Sei \vec F(\vec r) = \begin{pmatrix} \sin(y/2) \\ \cos(x/2) + y/8 \end{pmatrix} das betrachtete Vektorfeld und \vec \gamma(t) = \begin{pmatrix} t/2 – 2\sin(t) \\ -t/5 \end{pmatrix} mit \(t \in [a,b]\) für \(a,b \in \mathbb{R}\) der betrachtete Weg. Rechnen Sie nun das Wegintegral \(\int_\gamma \vec F \cdot d\vec s\) aus.
Hinweis: Das ist das Vektorfeld und der Weg aus dem obigen Video.
Zuerst bilden wir die Ableitung von \(\vec \gamma(t)\) nach \(t\). Diese lautet
\dot{\vec \gamma}(t) = \begin{pmatrix} 1/2 – 2 \cos(t) \\ -1/5 \end{pmatrix} \,.
Nun setzen wir in unser Vektorfeld \(\vec F\) den Weg ein. Dabei setzt man in alle \(x\)-Variablen des Vektorfeldes die \(x\)-Komponente des Weges ein. Das selbe macht man mit der \(y\)-Variablen des Vektorfeldes und der y-Komponente des Weges.
Hinweis: Die \(x\)- und \(y\)-Variablen sind immer dort, wo explizit ein \(x\) oder ein \(y\) steht. Die Komponenten eines Vektors sind die einzelnen Zeilen des Vektors.
Somit ergibt sich
\vec F(\vec \gamma(t)) = \begin{pmatrix} -\sin\left( \frac{t}{10} \right) \\ \cos\left( \frac{t}{4} – sin(t) \right) – \frac{t}{40} \end{pmatrix} \,.
Dabei wurde \(\sin(x) = -\sin(-x)\) genutzt.
Nun haben wir alle Faktoren, die wir brauchen, um das Wegintegral auszurechnen.
Mit obiger Definition des Wegintegrals ergibt sich
Nun tritt das Problem auf, dass dieses Integral wegen dem Term \( \frac{1}{5} \cos \left(\frac{t}{4} – \sin(t)\right) \) nicht analytisch lösbar ist. Wir müssen es also nummerisch lösen. Dies kann über selbst geschriebene Programme erfolgen (dies lernt man an der Georg-August-Universität in Göttingen in der Veranstaltung „Computergestütztes wissenschaftliches Rechnen“) oder man nutzt Wolfram Alpha.
Um das Integral in einem Intervall nummerisch mit der Hilfe von Wolfram Alpha zu lösen, benötigen wir feste Zahlen als Grenzen. Wir wählen hier willkürlich das Intervall \(t \in [5, 7] \). Damit ergibt sich
\[ \int_\gamma \vec F \cdot d\vec s \approx 1,41 \]
Der Befehl für Wolfram Alpha lautet hierbei „integrate [-0.5*sin(t/10) + 2*sin(t/10)*cos(t) – 1/5*cos(t/4-sin(t)) + t/200] dt from 5 to 7“
Wäre das Integral analytisch lösbar, würde man die Stammfunktion, wie aus der Schule gewohnt, ausrechnen, die Grenzen einsetzen, und das Ergebnis erhalten.
Es folgt ein Code-Beispiel, um das zu lösende Integral im willkürlich gewählten Intervall nummerisch mit Hilfe eines C-Programms zu lösen. Dazu sind Rechnungen und Umformung aus der obigen Lösung nötig.
Der Code kann in eine filename.c-Datei kopiert werden, und mit dem Befehl
gcc filename.c -o filename -lm; ./filename
in einem Terminal ausgeführt werden.
Code:
/* —– Bibliotheken —– */
#include<stdio.h>
#include<math.h>
/* —– Funktionen —– */
/* Nummerische Integration */
double riemann(double start, double end, int N, double funk(double)){
/*
Das Riemann-Verfahren ist ein einfaches nummerisches Verfahren
um die Fläche unterhalb einer Funktion auszurechnen.
Viele sollten es schon aus der Schule kennen.
*/
double intervall = (end-start)/N;
double sum = 0;
for(int i = 0; i < N; i++){
sum += funk(start + i * intervall);
}
sum *= intervall;
return sum;
}
double simpson(double start, double end, int N, double funk(double)){
/*
Das Simpson-Verfahren ist ein recht genaues nummerisches Verfahren
für nummerischen Integration; wesentlich genauer als das Riemann-Verfahren
welches viele aus der Schule kennen.
*/
double delta = (end-start)/N;
double sum = 0;
for (int i = 0; i < N; i++) {
sum += funk(start+i*delta) + funk(start+(i+1)*delta) + 4*funk(start+i*delta+delta/2.0);
}
sum *= delta/6;
return sum;
}
/* Integrand */
double f(double t){
return -0.5*sin(t/10) + 2*sin(t/10)*cos(t) – 1/5 * cos(t/4 – sin(t)) + t/200;
}
/* ===== Main-Funktion ===== */
int main(){
double a = 5;
double b = 7;
double flaeche = simpson(a, b, 10000, f); // ’simpson‘ kann durch ‚riemann‘ ersetzt werden, um anderes Verfahren zu testen.
printf(„Das Wegintegral für das Intervall [5,7] beträgt %lf.\n“, flaeche);
}
Verweise
Zu diesem Thema verweisen wir gerne auf folgende Seiten: